Naturliga logaritmen (logaritmus naturalis) förklaring


En speciell bas är e, basen för den naturliga logaritmen. Beteckningen för  är
är  .
.
Detta ger sambanden
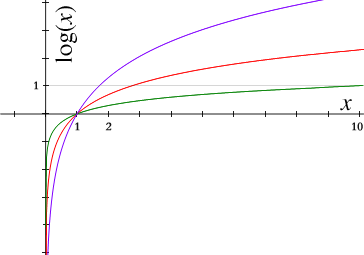
En viktig anledning till man använder denna logaritm är att den är den inversa funktionen till exponensfunktionen ex.
En intressant egenskap hos den naturliga logaritmfunktionen är att dess derivata är 1/x. Detta gör att den fyller ut en lucka bland de primitiva funktionerna till potensfunktioner:
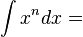

n = − 1 leder till division med noll, vilket är otillåtet. För varje tal nära − 1 kommer "första primitiva funktionen" att vara godtyckligt nära ln(x). Därför kan logaritmen ses som en kontinuerlig utvidgning av polynomen, ett faktum som även kan motiveras genom att betrakta vissa speciella gränsfall av interpolationspolynomen (kanske enklast via Newtons interpolationspolynom).
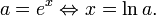


0 kommentarer:
Skicka en kommentar
Prenumerera på Kommentarer till inlägget [Atom]
<< Startsida